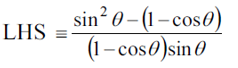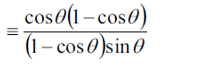国际课程提前学，A-Level数学之三角函数3：三角恒等式

An identity is different from an equation since an equation is only true for certain values of the variable, called the solution of the equation. The identity sign is kept for situations where we really want to emphasize that the relationship is an identity and not an equation.

恒等式与等式不同，一般的等式或者方程是在变量取某个或多个特定的值的时候，等式才成立，这个特殊值也称作方程的解。恒等式不同于等式，在定义域有意义的范围内，变量取任何值都成立。

The figure is a right-angled triangle which has hypotenuse of unit length. This gives rise to the definitions:

斜边为1的直角三角形的情况，

The Unit Circle

单位圆

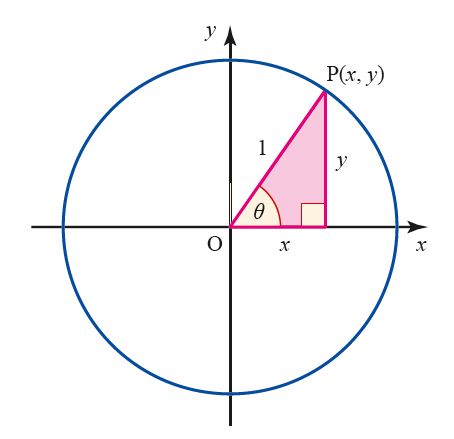
Now think of the angle θ being situated at the origin, as in the figure, and allow θ to take any value. The vertex marked P has co-ordinates (x,y) and can now be anywhere on the unit circle. We can now see that the definitions above can be applied to any angle θ, whether it is positive or negative, and whether it is less than or greater than 90°,

在单位圆中，圆心在原点，半径为1，角的终边与单位圆相交在点P，与X轴正半轴构成了角θ，不同于三角形范围内讨论角，在单位圆中，角的大小可以取任意实数，拓展了角的范围。

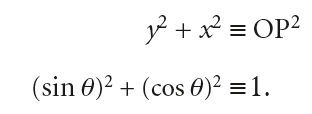
根据勾股定理，可以推导出恒等式。

Exercise （练习）

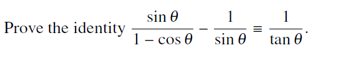
Solution: