400-616-8800
400-616-8800 400-616-8800
400-616-8800
Alevel数学干货,微积分之链式法则
1.The China rule (链式法则)
If y=f(u) is a differentiable function of u and u=g(x) is a differentiable function of x, then y=f(g(x)) is a differentiable function of x and
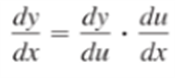
or, equivalently,
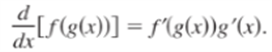
如果复合函数处处可导,可使用链式法则来进行求导,外部函数的导数乘以内部函数的导数。
常考题型解析:
Example 1
![]()
SOLUTION
As you saw earlier, you can break down this expression as follows.
![]()
Differentiation these gives
![]()
and
![]()
By the chain rule

2. Related-Rate Problems
相关变化率问题
Differentiation with respect to different variables
对于不同变量的微分
The chain rule makes it possible to differentiate with respect to a variable which does not feature in the original expression. For example, the volume V of a sphere of radius r is given by
![]()
Differentiating this with respect to r gives the rate of change of volume with radius,
![]()
However you might be more interested in finding dv/dt, the rate of change of change of volume with time, t. To find this, you would use the chain rule:
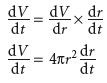
相关变化率问题是复合函数求导的应用,例,半径为r的球体积为
![]()
体积对半径进行微分,可得到体积对于半径的变化率,
![]()
要求出体积对于时间的变化率dV/dt,可以使用链式法则,通过半径r对时间t进行微分。
常考题型解析
Example 2