A-level数学干货，微积分之函数增减性

1. Increasing and Decreasing Functions  增函数与减函数

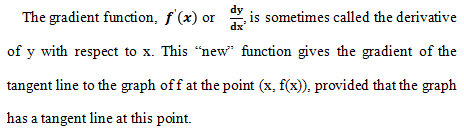
导数是函数的斜率组成的新函数，可以得到过曲线上任一点的切线斜率。可以说导数决定了函数的增减性，函数的增减性也决定这导数的正负。

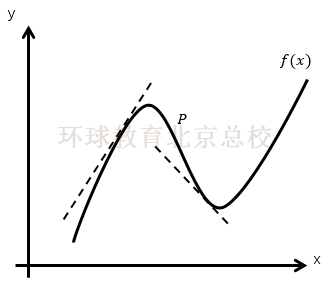
请输入正文

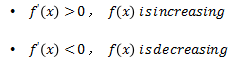
当导数大于零，函数是增函数；当导数小于零，函数是减函数。

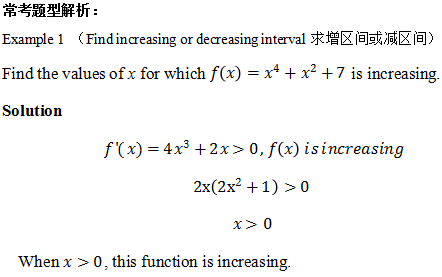
2. 最大值与最小值问题

Maxima and Minima Problems

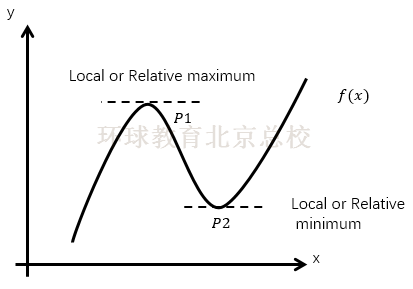
P1 is called a local or relative maximum point，p2 is called a local or relative maximum point. The gradient of the tangent line at a maxima or minima is zero, or does not exist.  

点P1称为局部最大值或相对最大值，P2称为局部最小值或相对最小值。最大或最小值处的切线斜率为零，或者斜率不存在。

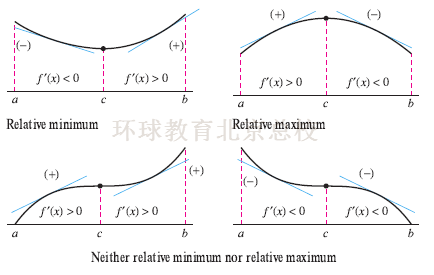
一阶导数测试是决定函数转折点性质的常规方法，假设函数f（x）在包含点C的区间内连续，点C的导数为零，或者C处不可导，

如果导数在穿过点c时由正变负，则函数在点C处有相对最大值；

如果导数在穿过点c时由负变正，则函数在点C处有相对最小值；

如果导数在点c两侧同时为正或为负，则函数在点C处没有相对极值出现。

常考题型解析

Example 2（求函数的相对极值/驻点问题）

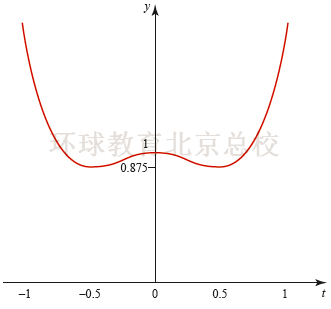
解题步骤：

1. 一阶导数为零，求出关键点；

2. 带回原函数，求出函数值；

3. 通过一阶段测试，觉得关键点的性质, 最大值，最小值，或者不是极值点。

函数的增减性与一阶导数紧密联系在一起，求函数的极值问题无论在考试中还是在生活应用中都是非常重要的。下一期，我们会深化学习，讨论二阶导数与函数凹凸性的关系。